Precal Fall 2013 Final Exam (PDF)
File information
This PDF 1.5 document has been generated by LaTeX with hyperref package / pdfTeX-1.40.12, and has been sent on pdf-archive.com on 08/12/2014 at 20:18, from IP address 72.177.x.x.
The current document download page has been viewed 1061 times.
File size: 153.6 KB (11 pages).
Privacy: public file



File preview
MATH 2312
Fall 2013
Final Exam
Name:
Date:
You must show enough of your work so that the grader can follow what you did. If it is possible to find an exact answer by
taking an algebraic approach, you may not receive full credit for an approximation or a calculator-generated answer.
1. Use the graph of f (x) to the right to find or estimate
(a) f (4)
(b) f −1 (4)
(c) (f ◦ f )(8) = f (f (8))
(d) the average rate of change of f (x) with respect to x as x
changes from 0 to 8.
2. Use the graph to the right to answer the following questions.
(a) Find an equation of the line L1 .
(b) Find an equation of the line L2 which is perpendicular to the line
L1 .
(c) Find the point of intersection of the two perpendicular lines.
3. Use the two tables below to answer the questions that follow.
x
y
3
5
2
4
1
1
0
2
1
1
2
0
3
-2
X
Y
-3
5
-2
4
-1
1
0
2
1
1
2
0
3
-2
(a) Is y a function of x? Yes or no? (Circle one)
(a) Is Y a function of X? Yes or no? (Circle one)
(b) Why?
(b) Why?
4. The two tables below define functions f and g. Answer the questions that follow.
x
f (x)
-3
-6
-2
-4
-1
-2
0
0
1
2
2
4
3
6
x
g(x)
(a) Does f have an inverse? Explain your answer
5. Find and simplify
-3
5
6. Find the domain of the function f (x) =
x+4
x
-1
1
0
0
1
2
2
3
3
6
(a) Does g have an inverse? Explain your answer
f (x + h) − f (x)
, where h 6= 0, if f (x) = x2 − x.
h
√
-2
3
1
1
and g(x) =
, find the composite function (f ◦ g)(x) = f (g(x)). Simplify
x+1
3x − 1
until you have a rational function.
7. Given that f (x) =
8. The graph of the quadratic function f shown in the figure has vertex at (2, 1) and y-intercept at (0, 7).
(a) Find a formula for the function f .
(b) On the same axes, graph the function g(x) = f (x + 1) + 3.
9. Using the Rational Zeros Theorem, list all the possible rational zeros of the function f (x) = −2x3 + 2x2 − 3.
Do not solve the equation!
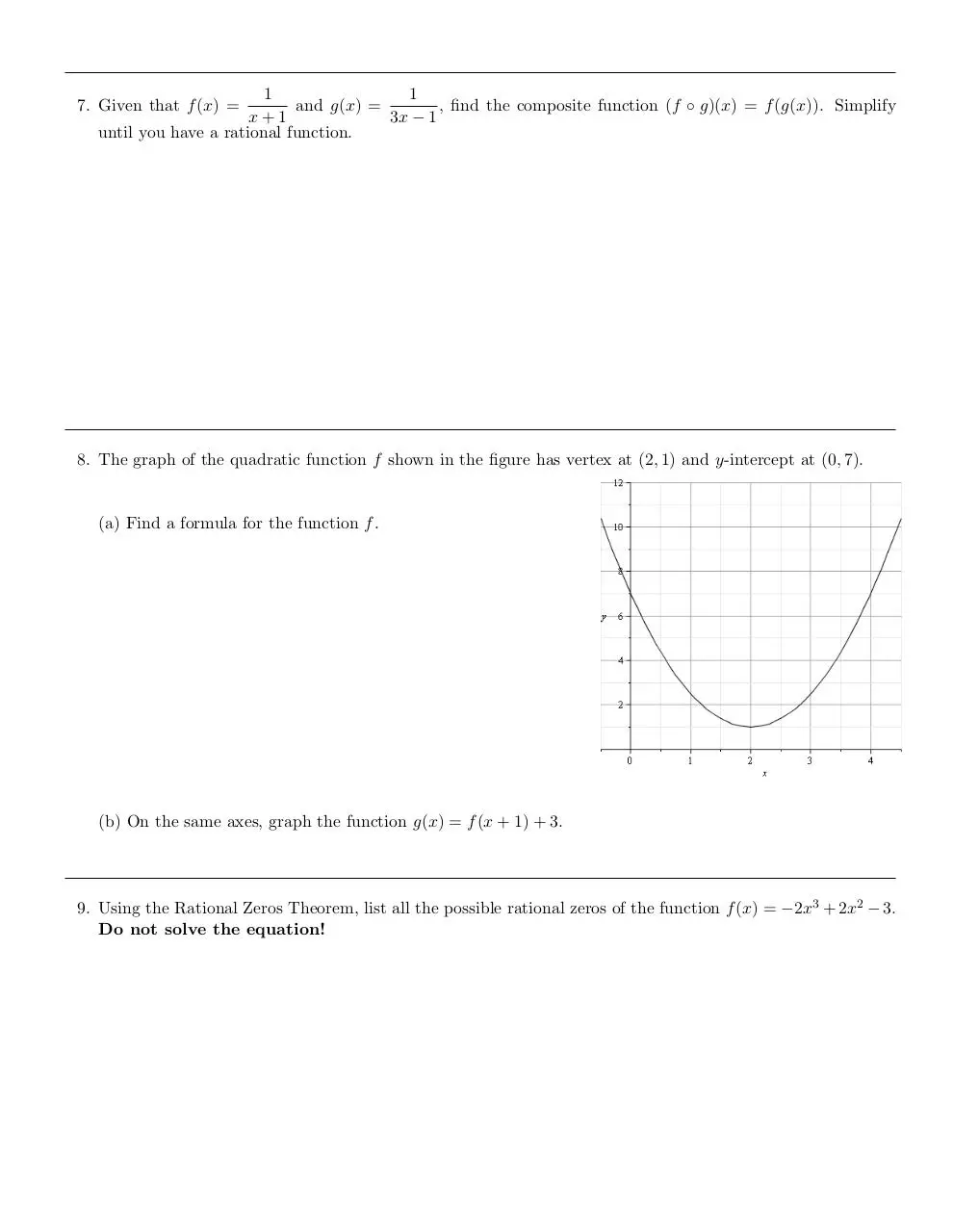
10. To the right is a graph of the polynomial function P (x).
(a) What might the degree of the polynomial be? Why?
(b) Find a possible formula for P (x).
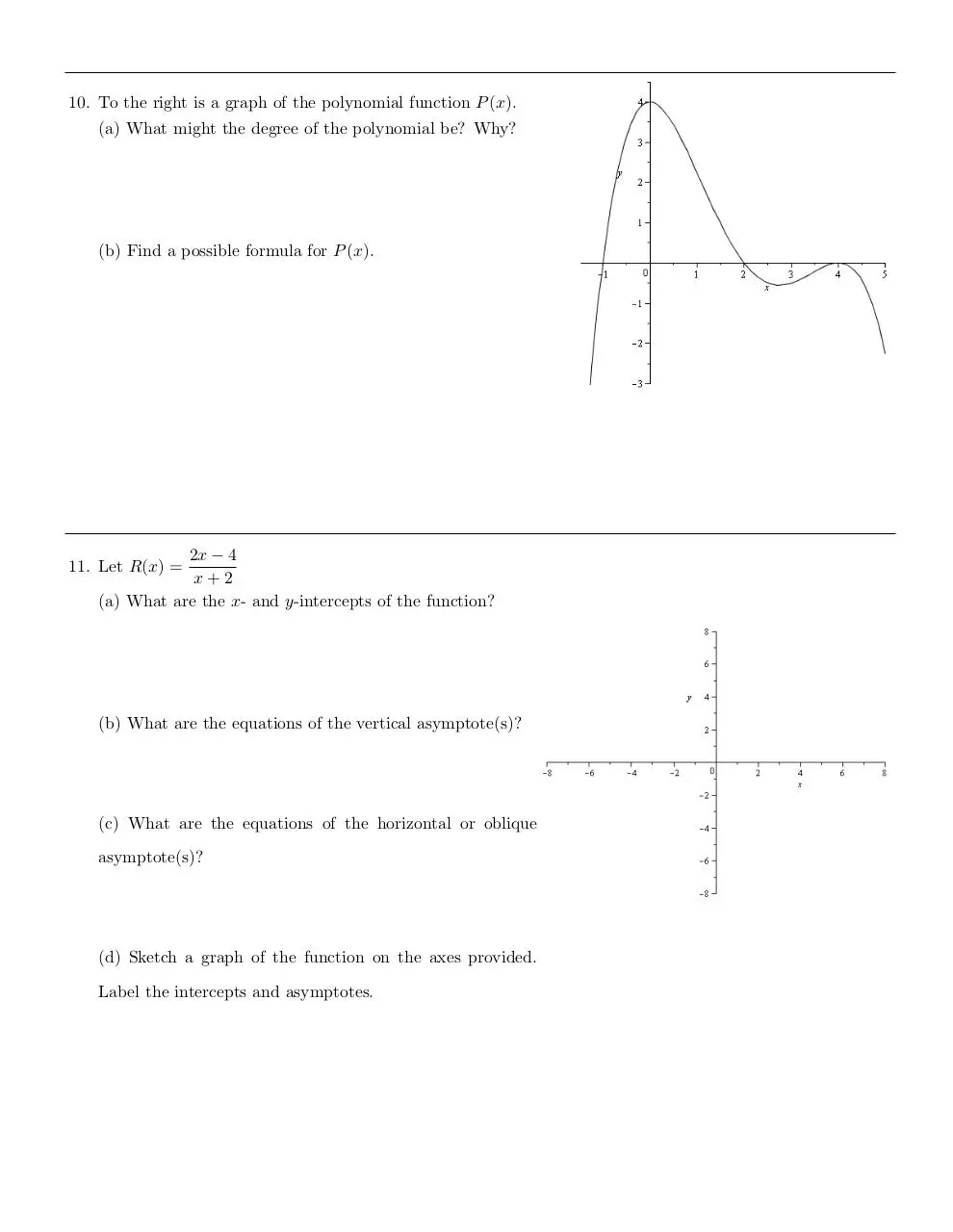
2x − 4
x+2
(a) What are the x- and y-intercepts of the function?
11. Let R(x) =
(b) What are the equations of the vertical asymptote(s)?
(c) What are the equations of the horizontal or oblique
asymptote(s)?
(d) Sketch a graph of the function on the axes provided.
Label the intercepts and asymptotes.
12. Use polynomial division to simplify the following rational expression.
2x4 + 3x3 + 5x2 + 9x − 3
x2 + 3
13. Use the properties of logarithms to answer the following questions.
r
(a) Expand the expression as a sum, difference, and/or constant multiple of logarithms. log7
(b) Condense the expression to the logarithm of a single quantity. 3 log3 x − 4 log3 y + 2 log3 z
x4 y
z 10
!
14. Let f (x) = ln(x + 4). Find a formula for the inverse function of f .
15. Solve the equations for x:
(a) log5 (6x + 7) = 2
(b) ln(x) − ln(x − 1) = 3
2
16. Solve the equation for x: 4x = 162x .
17. A principal, P , of $5, 000 is invested at the nominal annual rate of r = 5% compounded quarterly. What
will be the balance of the investment after 20 years?
18. The number of bacteria growing in an incubation culture increases with time according to the formula
N (t) = 5200(5)t , where t is time measured in days. After how many days will the number of bacteria in the
culture be 650,000?
19. Suppose a Gross Unknown Material (GUM) is radioactive and has a half-life of 20 days. What is the rate of
decay of GUM expressed as a percentage? Round your answer to two decimal places.
2
20. Find the exact value of each of the remaining 5 trigonometric functions of θ if cos(θ) = and θ is in the 4th
5
quadrant.
21. Below is given the graph of a trigonometric function. Fill in the blanks and answer part (d).
(a) The amplitude is
(b) The midline is y =
(c) The period is
(d) Give a possible formula for the function.
22. While watching a softball game, Sean notices a blimp straight ahead and above him at an angle of elevation
of 48◦ . Three minutes later, he notices the blimp is still straight ahead, but now at an angle of elevation of
35◦ . If the blimp maintained an altitude of 2000 feet, how far did the blimp travel in those three minutes?
23. Find all solutions of the following equation in the interval 0 ≤ θ < 2π.
2 sin2 (θ) = 2 + cos(θ)
Download Precal - Fall 2013 - Final Exam
Precal - Fall 2013 - Final Exam.pdf (PDF, 153.6 KB)
Download PDF
Share this file on social networks
Link to this page
Permanent link
Use the permanent link to the download page to share your document on Facebook, Twitter, LinkedIn, or directly with a contact by e-Mail, Messenger, Whatsapp, Line..
Short link
Use the short link to share your document on Twitter or by text message (SMS)
HTML Code
Copy the following HTML code to share your document on a Website or Blog
QR Code to this page

This file has been shared publicly by a user of PDF Archive.
Document ID: 0000198172.