Formelsammlung FL .pdf

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Grundlagen
Spannungen
F
= n (S. 3)
A

=

Ft
A

σ:
τ:
F:
A:

(S. 3)

Einachsiger Spannungszustand nur  !

[

 j , k=

 x  xy
 yx  y

]

Normalspannung
Tangentialspannung
Kraft
Fläche

(S. 9)

Spannungstensor zweiachsig

[

 x  xy  xz
 j , k =  yx  y  yz
 zx  zy  z
Spannungstensor dreiachsig

]



(S. 9)



  y
 − y
I ,I I= x
± 2xy  x
2
2
2
2
 x = I⋅cos  I I⋅sin 
2
2
 y = I⋅sin  I I⋅cos 
 xy = yx= I − I I ⋅sin⋅cos 
  y
M= x
2
 − I I
R= I
2



2

σ:
τ:
M:
R:

Normalspannung
Tangentialspannung
Kreismittelpunkt
Kreisradius

(S. 11)

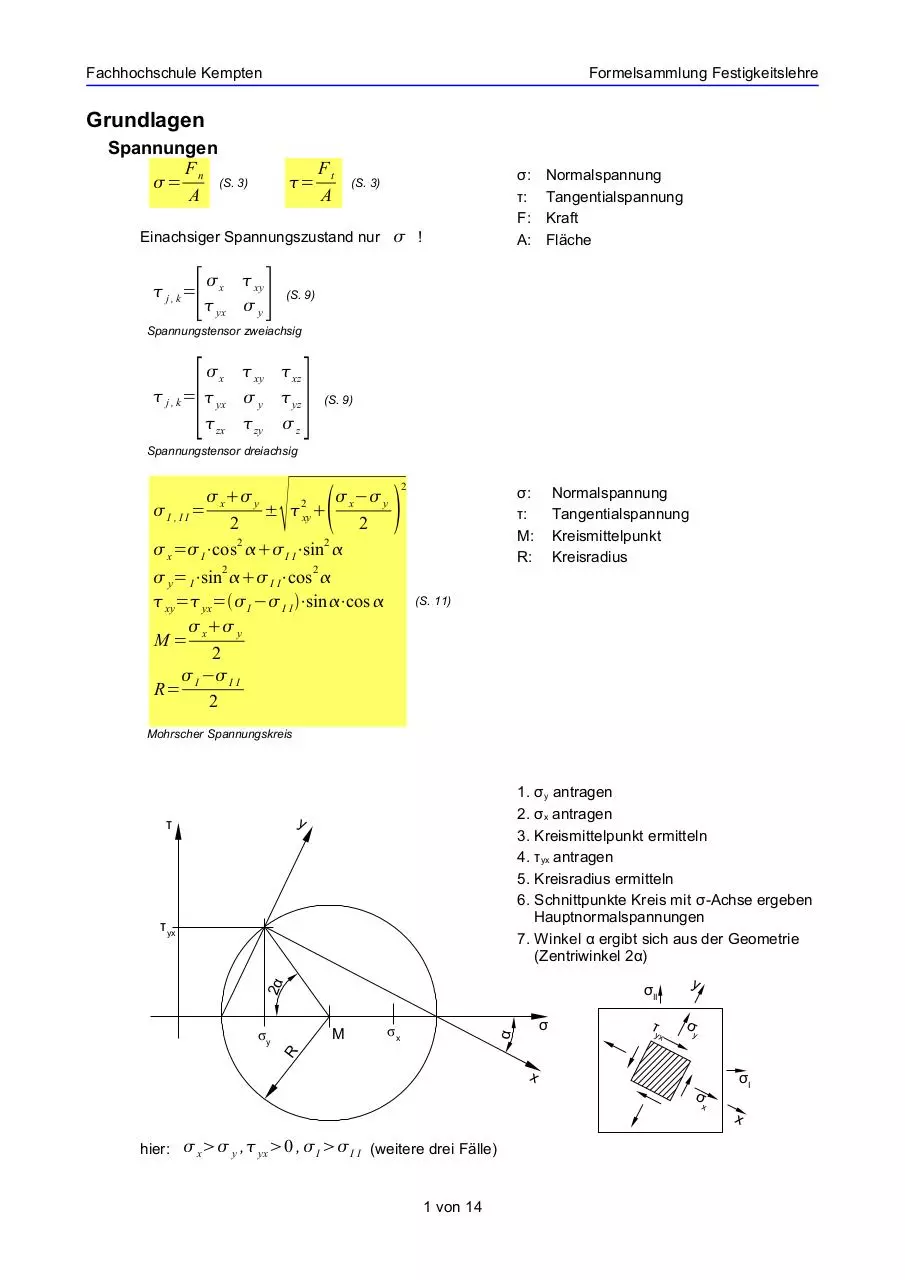
Mohrscher Spannungskreis

1. σy antragen
2. σx antragen
3. Kreismittelpunkt ermitteln
4. τyx antragen
5. Kreisradius ermitteln
6. Schnittpunkte Kreis mit σ-Achse ergeben
Hauptnormalspannungen
7. Winkel α ergibt sich aus der Geometrie
(Zentriwinkel 2α)

y

τ

2α

τyx

σx

σ

τy

x

σ

y

R

α

M

σy

y

σII

x
σ

x

hier:

 x  y ,  yx 0 ,  I  I I (weitere drei Fälle)
1 von 14

σI
x

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Verformungen (Dehnung)
l
=el  T
(S. 31)
=
l
l =


E

q =−⋅

(S. 37)

Zugversuch

ε:
εel:
ε l:
ε q:
εV:
εΔT:
σ:
E:
Δl:
l:
ν:

(S. 37)

Zugversuch

 x  y  z
⋅1−2 
2
V ≈ x  y  z
V =

1
 x = ⋅[  x −⋅ y  z  ]
E
1
 y = ⋅[  y −⋅ z  x  ]
E
1
 z = ⋅[  z −⋅ x  y  ]
E

(S. 32/38)

Dehnung
elastische Dehnung
Längsdehnung
Querdehnung
Volumendehnung
Temperaturdehnung
Normalspannung
Elatizitätsmodul, E-Modul
Längenänderung
Ausgangslänge
Querkontraktionszahl

(S. 38)

für dreiachsigen Spannungzustand

=00,5

(S. 40)

Spannungen durch Dehnungen ausgedrückt
 x = x⋅E (S. 39)
einachsig

E
⋅ x ⋅ y 
1− 2
E
 y=
⋅ y ⋅ x 
1− 2
 x=

(S. 39)

zweiachsig

E
⋅[ 1−⋅ x ⋅ y  z  ]
1⋅1−2 
E
 y=
⋅[ 1−⋅ y ⋅ z  x  ]
1⋅1−2 
E
 z=
⋅[ 1−⋅ z ⋅ x  y  ]
1⋅1−2 
 x=

(S. 39)

dreiachsig

Festigkeitsverhalten der Werkstoffe
Hook'sches Gesetz


tan = =E


α:
ε:
σ:
E:

(S. 37)

2 von 14

Neigung der Hook'schen Geraden
Dehnung
Normalspannung
Elatizitätsmodul, E-Modul

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

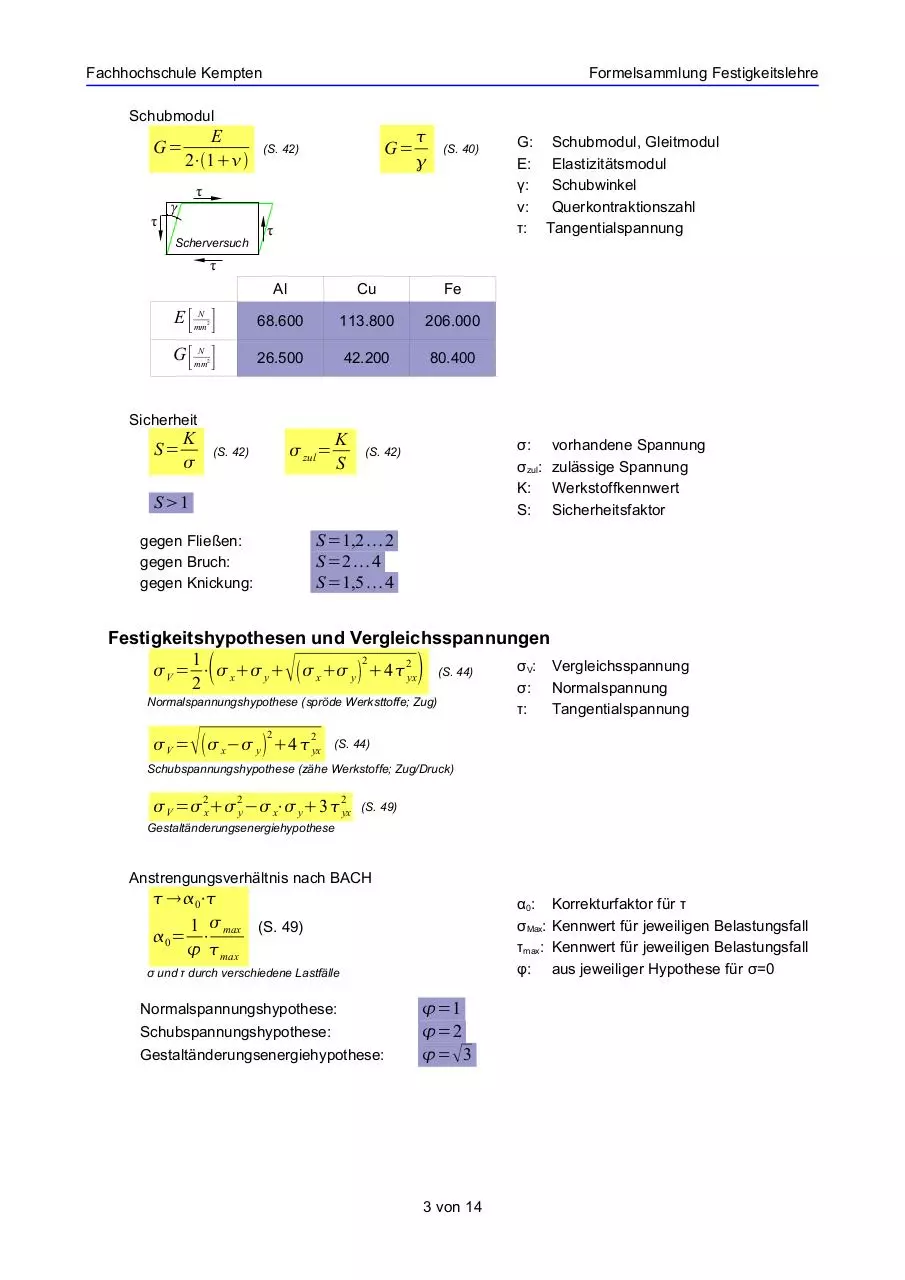
Schubmodul

G=

τ

E
2⋅1

G=

(S. 42)




(S. 40)

τ

γ

Scherversuch

τ

G: Schubmodul, Gleitmodul
E: Elastizitätsmodul
γ: Schubwinkel
ν: Querkontraktionszahl
τ: Tangentialspannung

τ
Al

Cu

Fe

E [ mmN ]

68.600

113.800

206.000

G [ mmN ]

26.500

42.200

80.400

2

2

Sicherheit

S=

K


K
S

 zul =

(S. 42)

σ:
σzul :
K:
S:

(S. 42)

S 1

vorhandene Spannung
zulässige Spannung
Werkstoffkennwert
Sicherheitsfaktor

S =1,22
S =24
S =1,54

gegen Fließen:
gegen Bruch:
gegen Knickung:

Festigkeitshypothesen und Vergleichsspannungen
2
1
σV: Vergleichsspannung
 V = ⋅  x  y    x  y  4 2yx (S. 44)
2
σ: Normalspannung







Normalspannungshypothese (spröde Werksttoffe; Zug)



2

 V =   x − y  4  yx
2

τ:

Tangentialspannung

α0:
σMax:
τmax:
φ:

Korrekturfaktor für τ
Kennwert für jeweiligen Belastungsfall
Kennwert für jeweiligen Belastungsfall
aus jeweiliger Hypothese für σ=0

(S. 44)

Schubspannungshypothese (zähe Werkstoffe; Zug/Druck)

 V = 2x  2y − x⋅ y 3 2yx

(S. 49)

Gestaltänderungsenergiehypothese

Anstrengungsverhältnis nach BACH

  0⋅
1 
(S. 49)
0= ⋅ max
 max
σ und τ durch verschiedene Lastfälle

Normalspannungshypothese:
Schubspannungshypothese:
Gestaltänderungsenergiehypothese:

=1
=2
=  3

3 von 14

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Schnittlasten
Allgemein

Q=−

dM
dx

dQ
dx

q=

Q:
q:
M:
N:
x:

(S. 51)

q(x)

Querkraft
Streckenlast
Moment (Biegemoment)
Normalkraft
Bauteillänge

dx

Definition Schnittufer

q(x)

M

M+dM

N
Q

M

Q+dQ

Ι

+

N+dN

Q

N

M

-

N
Q

dx
Klammerfunktion (FÖPPL-Symbol)

{

〈 x−x i 〉n =
mit :

0 für x x i

x:
x i:

n

〈 x− x i 〉 für x x i

Laufvariable
Bereichsvariable

(S. 66)

{

0 für xx i
n=
1 für x x i
d
〈 x−x i 〉n =n⋅〈 x− x i 〉n−1
dx
1
⋅〈 x− x i 〉n1
∫ 〈 x− xi 〉n dx= 1n

(S. 66)

Beanspruchung stabförmiger Bauteile
Zug- und Druckbeanspruchung
F
(S. 68)
=
E⋅A

αK:

Stäbe mit konstantem Querschnitt und konstanter Längskraft



⋅g⋅ l⋅x−
 l=

E

x2
2



(S. 70)

Stäbe mit veränderlicher Last und konstantem Querschnitt

 x=

F
E⋅A x

(S. 73)

Stäbe mit konstanter Last und veränderlichem Querschnitt

F
A
 max = K⋅ n
 n=

(S. 74)

Stäbe mit Geometrie- und / oder Laständerung

4 von 14

Spannungskonzentrationsfaktor
(Kerbfaktor)
ε:
Dehnung
ρ: Dichte des Werkstoffes
σn: Nennspannung
σmax: Maximalspannung
A: Fläche
E: Elatizitätsmodul, E-Modul
F: Kraft
g: Erdbeschleunigung
l:
Ausgangslänge
x: Laufvariable

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

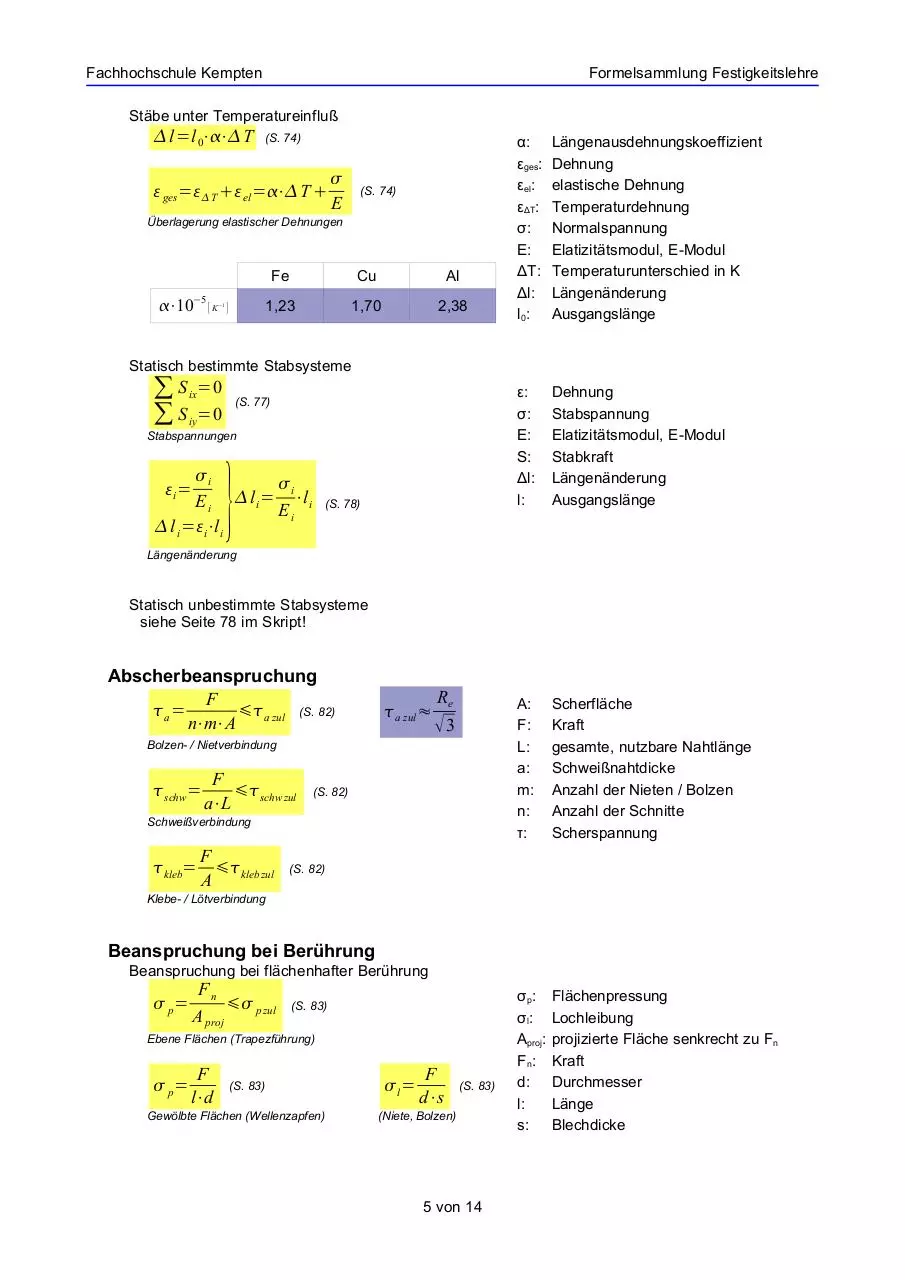
Stäbe unter Temperatureinfluß

 l=l 0⋅⋅T

(S. 74)

 ges =T el =⋅T 


E

(S. 74)

Überlagerung elastischer Dehnungen

−5

⋅10

[ K −1 ]

Fe

Cu

Al

1,23

1,70

2,38

α:
εges:
εel:
εΔT:
σ:
E:
ΔT:
Δl:
l0:

Längenausdehnungskoeffizient
Dehnung
elastische Dehnung
Temperaturdehnung
Normalspannung
Elatizitätsmodul, E-Modul
Temperaturunterschied in K
Längenänderung
Ausgangslänge

ε:
σ:
E:
S:
Δl:
l:

Dehnung
Stabspannung
Elatizitätsmodul, E-Modul
Stabkraft
Längenänderung
Ausgangslänge

A:
F:
L:
a:
m:
n:
τ:

Scherfläche
Kraft
gesamte, nutzbare Nahtlänge
Schweißnahtdicke
Anzahl der Nieten / Bolzen
Anzahl der Schnitte
Scherspannung

σ p:
σl:
Aproj:
F n:
d:
l:
s:

Flächenpressung
Lochleibung
projizierte Fläche senkrecht zu Fn
Kraft
Durchmesser
Länge
Blechdicke

Statisch bestimmte Stabsysteme

∑ S ix=0
∑ S iy=0

(S. 77)

Stabspannungen

}

i
i
E i  l i = E ⋅l i
i
 l i =i⋅l i
i =

(S. 78)

Längenänderung

Statisch unbestimmte Stabsysteme
siehe Seite 78 im Skript!

Abscherbeanspruchung
F
a =
 a zul (S. 82)
n⋅m⋅A

a zul ≈

Bolzen- / Nietverbindung

 schw=

F
 schw zul
a⋅L

Re

3

(S. 82)

Schweißverbindung

 kleb=

F
 kleb zul
A

(S. 82)

Klebe- / Lötverbindung

Beanspruchung bei Berührung
Beanspruchung bei flächenhafter Berührung

 p=

Fn
 p zul
A proj

(S. 83)

Ebene Flächen (Trapezführung)

 p=

F
l⋅d

(S. 83)

Gewölbte Flächen (Wellenzapfen)

l=

F
d⋅s

(S. 83)

(Niete, Bolzen)

5 von 14

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Beanspruchung bei linien- / punkthafter Berührung (Hertz'sche Pressung)

r=

r 1⋅r 2
r 1r 2

E=





E 1⋅ 1− E 2⋅ 1−
2
2

3⋅F⋅r
a=
2⋅E



Zylinder



F⋅E
2⋅r⋅l
8⋅r⋅F
a=
⋅l⋅E

Querkontraktionszahl
Druckspannung
Elastizitätsmodul der Berührstelle
Kraft
halbe Breite / Radius der Berührfläche
Berührungslänge
Radius

Kugel

r1

r2

(S. 84)

da

r2  ∞

Berührfläche
2a

(S. 84)

positiv
r2

Zylinder gegen Zylinder

r=r 1

Radius

r1

l



ν:
σD:
E:
F:
a:
l:
r:

(S. 84)

Kugel gegen Kugel

 D=

2
1

2

1 3 3⋅F E
 D= ⋅
⋅
2
r




2⋅E 1⋅E 2

negativ

2a

Kugel / Zylinder gegen Ebene

Biegebeanspruchung
Flächenträgheitsmoment
(S. 86)

y

dA
x

z

I =I z a 2⋅A

A

η

(S. 93)

y

Koordinatenursprung im Schwerpunkt

a

I z =∫ y 2⋅dA

Koordinatenverschiebung (parallele Achsen); Satz von STEINER





(S. 113)

Koordinatenverdrehung; Mohr'scher Trägheitskreis

1. Iy antragen
2. Iz antragen
3. Kreismittelpunkt ermitteln
4. Izy antragen
5. Kreisradius ermitteln
6. Schnittpunkte Kreis mit I-Achse ergeben
Hauptflächenträgheitsmomente
7. Winkel α ergibt sich aus der Geometrie
(Zentriwinkel 2α)

z

y

Iz

M

Iy

II

I

R

Iz

α

2α

y

III

Flächenträgheitsmoment um η
Flächenträgheitsmoment um z
Zentrifugalmoment
polares Flächenträgheitsmoment
Abstand z-Achse zu η-Achse
Fläche

2

I I
I y I z
I I ,I I= y z ±
I 2zy
2
2
2⋅I zy
tan 2 =
I y −I z
I p =I y I z = I I I I I

Iz

Iη :
Iz:
Izy:
Ip :
a:
A:

y

6 von 14

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Zentrifugalmoment

I yz =∫ y⋅z⋅dA

Iyz:
A:
S:

(S. 111)

A

Koordinatenursprung im Schwerpunkt

I yz = I yz  y s⋅z s⋅A

(S. 114)

Zentrifugalmoment
Fläche
Schwerpunkt
dA

Koordinatenverschiebung; Satz von STEINER

y
S

I yz =0 !

für symmetrische Bauteile

y

z

z

y

ys

A
z

zs

x

Einfache Biegeformel (anwendbar für Iyz=0)

I z =∫ y ⋅dA
I
W z= z
y max
M
 x =− ⋅y
Iz
M
M
 max = ⋅y max =
Iz
Wz
2

σd

M

Iz:
W z:
ymax:
y:
M:
σmax:
σx:
dA:

(S. 86)

y

axiales Flächenträgheitsmoment
Widerstandsmoment
maximaler Randfaserabstand
Faserabstand
Biegemoment
Maximalspannung
Biegespannung
Flächenelement

M

z

x

σz

Schiefe Biegung (doppelte Biegung bei Kreisquerschnitten)

M b=  M 2z M 2y
M
tan = z
My
Mb
=±
⋅z
Iy 1

 
 

y

y1

(S. 100)

z

1

 max =±

My

Mb

Mb
⋅R
Iy

x

Mz

α
R

z1

Iy1:
Mb :
My:
Mz:
R:
α:
σ:

Flächenträgheitsmoment
resultierendes Moment
Momemte in y-Richtung
Momemte in z-Richtung
Radius des Kreisquerschnittes
Winkel der Koordinatendrehng
Biegespannung

1

Schiefe Biegung (Profile mit zwei zueinander senkrechten Achsen)

Mz
M
⋅y max ± y⋅z max
Iz
Iy
M
M
=± z ± y
Wz Wy

Iy/z: Flächenträgheitsmomente
My: Momemte in y-Richtung
Mz: Momemte in z-Richtung
W y/z: Widerstandsmomente
σ: Biegespannung
ymax: maximaler Randfaserabstand in y
zmax: maximaler Randfaserabstand in z

=±

(S. 103)

7 von 14

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Schubspannungen in symmetrischen Querschnitten

mittel =

Q
A

3
max = ⋅mittel
2

(S. 119)

Rechteckquerschnitt

4
max = ⋅mittel
3
Kreisquerschnitt

max =2⋅mittel

τ:
Q:
A:

Schubspannung
Querkraft
Fläche

E:
I:
E*I:
M:
Q:
f:
q:
w'':
α:

Elastizitätsmodul
Flächenträgheitsmoment
Biegesteifigkeit
Biegemoment
Querkraft
maximale Durchbiegung
Streckenlast
Krümmung der Biegelinie
Winkel der Durchbiegung

(S. 119)

Kreisringquerschnitt

Durchbiegung von Trägern

w ''=−

M
E⋅I

(S. 135)

Gleichung der elastischen Linie

w '''=−

Q
E⋅I

w ''''=−

wmax = f

q
E⋅I

w' =

f und α aus Tabellen!

Torsionsbeanspruchung
Stäbe mit Kreis(ring)querschnitt und konstantem Durchmesser

=

M t⋅l
G⋅I p

max =

Mt
Wt

Am: von der Profilmittellinie
eingeschlossene Fläche
G: Schubmodul
Ip: polares Flächenträgheitsmoment
Mt: Torsionsmoment
T: Schubfluß (pro Längeneinheit)
W t: Widerstandsmoment der Torsion
c: Drehfederkonstante
l:
Bauteillänge
t:
Wanddicke
s:
τ:
Schubspannung
φ: Verdrehwinkel

(S. 165)

Torsion einer abgesetzten Welle

1
1
=∑
c
ci

=

Mt
c

(S. 173)

Stäbe mit Kreisquerschnitt und veränderlichem
Durchmesser

W t=
=

I t  x
r  x

=∫

M  x
⋅dx
G⋅I p  x

(S. 179)

Mt
Wt

Dünnwandige, geschlossene Profile mit beliebigem Querschnitt

M t =2⋅⋅t⋅A m

W t =2⋅t min⋅A m

(S. 187)

(S. 188)

T =⋅t

(S. 184)

1.Bredt'sche Formel

Mt
M
max =
= t
2⋅t min⋅A m W t

(S. 188)

ds
∫
M ⋅l
t  s
= t ⋅
G
4⋅A 2m
2. Bredt'sche Formel


=Drillung (S. 190)
l

4⋅A2m⋅t
I t=
Umfang
für t=const.

8 von 14

(S. 190)

4⋅A2m
I t=
∫ t ds
 s

(S. 190)

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Dünnwandige offene Profile (Flachmaterial)

1
I t = ⋅b3⋅h
3
max =

1
W t = ⋅b 2⋅h
3

(S. 192)

3⋅M t
2

b ⋅h

=

(S. 192)

Mt
⋅l
G⋅I t

Allgemein für dünnwandige offene Profile


I t = ⋅∑ hi⋅bi3
3

(S. 192)

W t=

It
b max

b:
h:
l:
G:
I t:
Mt :
W t:
τ:
φ:
η:

kleine Abmessug des Rechtecks
große Abmessung des Rechtecks
Bauteillänge
Schubmodul
polares Flächenträgheitsmoment
Torsionsmoment
Widerstandsmoment der Torsion
Schubspannung
Verdrehwinkel
Konstante aus Tabelle

Zusammengesetzte Beanspruchung
(S. 195ff)

Biegung und Normalkraft können direkt addiert werden, da beides Normalspannungen sind!

 1,2 =−

N M
∓
A W

Bei Biegung und Schub müssen Vergleichsspannungen (siehe Seite 3) ermittelt werden, welche
kleiner sein muß als die zulässige Spannung.
Bei Biegung und Torsion müssen an gezielten Punkten Vergleichsspannungen (siehe Seite 3)
ermitelt werden. Und zwar an den Stellen mit der größten Spannung.
Bei Längskraft und Torsion muß eine Vergleichsspannung (siehe Seite 3) am Rand ermittelt
werden, da dort die größten Spannungen sind.
Bei Schub und Torsion können die Spannungen direkt addiert werden, aber es muß auf die
Richtung geachtet werden.
Bei Biegung, Schub, Längskraft und Torsion analog der vorhergehenden Beispiele.

Dünnwandige Bauteile
Dünnwandige Ringe
Dünnwandiger Ring unter Innen- oder Außendruck

 t=

pi⋅d i
2⋅t

 t =−

(S. 211)

Innendruck

p a⋅d a
2⋅t

Außendruck

d
 t = pi − p a ⋅
2⋅t

d:
p:
t:
σ t:

Durchmesser
Druck
Wandstärke
Tangentialspannung

r:
E:
T:
α:
σ:

Zylinderradius
E-Modul
Temperatur
Längenausdehnungskoeffizient
Spannung

r:
v:
σ:
ρ:
ω:

Ringradius
Geschwindigkeit
Spannung
Dichte
Winkelgeschwindigkeit

(S. 211)

Näherungsformel

Kreiszylinder unter Temperatureinfluss (und Spannung)






 r= ⋅T ⋅r
E

(S. 213)

Kreiszylindrischer Ring unter Fliehkraft

 t =⋅v 2

(S. 217)

v=r⋅

=

⋅n
30

9 von 14

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Dünnwandige Behälter
Kreiszylindrischer Behälter unter Innen- oder Außendruck

pi⋅d
4⋅t

 a=

t=

(S. 219)

axiale Richtung

pi⋅d
2⋅t

(S.219)

Umfangsrichtung

 t =2⋅ a

d:
p:
t:
σ:

Behälterdurchmesser
Druck
Wanddicke
Spannung

d:
p:
t:
σ:

Behälterdurchmesser
Druck
Wanddicke
Spannung

bei Außendruck: Sigma negativ
Kugelbehälter unter Innen- oder Außendruck

=

pi⋅d
4⋅t

(S. 221)

1
 max = ⋅ max
2
Kugel

Zylinder

Stabilitätsprobleme
Knickung
Knickspannungsdiagramm
σK
σd

1: Quetschen
2: plastisches Knicken (Tettmair)
3: elastisches Knicken (Euler)

Quetschgrenze

a

Tettmair-Gerade
(für Grauguss Parabel)

σdF

a: σd-Abschnitt der Tettmair-Gerade
b: Steigung der Tettmair-Gerade

σdP

Euler-Hyperbel (σK)
1

2

λF

F=

3

λP

λ



a− dF
b

 P =⋅

Material

E [ mmN ]

S235

2,1*105

E335

5

GG20

E
 dP
a [ mmN ]

b [ mmN ]

104

310

1,14

0

2,1*10

89

335

0,62

0

1,0*10

80

776

12

0,05

P

2

5

2

10 von 14

2

c [ mmN ]
2

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Knickung im elastischen Bereich (Euler-Bereich)

F
⋅w=0
E⋅I

(S. 225)

Differentialgleichung



F
⋅l=n⋅
E⋅I

(S. 226)

n. Eigenwert, Eigenform der Knickung

mit

n=1

F K=

folgt

2⋅E⋅I min

(S. 226)

l 2K

Eulersche Knicklast



I min
A

=

(S. 226)

Trägheitsradius



lK
i min

(S. 226)

Trägheitsradius
Knicklänge
Durchbiegung
Querschnitt
E-Modul
Knicklast
Flächenmoment des kleinsten A
Sicherheit gegen Knicken
Schlankheitsgrad
Druck-Fließgrenze
Druck-Proportionalitätsgrenze
Knickspannung

Schlankheitsgrad

F K 2⋅E
K= = 2
A


 dP =

(S. 226)

Knickspannung (Euler-Hyperbel)

F 
 d vorh =  K
A SK

2⋅E
2P

(S. 227)

Druck-Proportionalitätsgrenze

I min

(S. 230)

Festigkeitsbedingung

F vorh⋅l 2K⋅S K
2⋅E

(S. 229)

Mindestflächenmoment

S K =510

 dP≈0,8⋅ dF
Die vier Eulerfälle (Knicklängen)

F

F

F

lK = l

l K= 2 l

l

F

11 von 14

lK ≈ 0,7 l

i min =

i:
l:
w:
A:
E:
F:
Imin:
SK:
λ:
σdF:
σdP:
σK:

lK = 0,5 l

w' '

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Knickung im plastischen Bereich (Tettmair-Bereich)

 K =a−b⋅

(S. 231)

Knickspannunng für Stahl

 K =a−b⋅c⋅2

(S. 231)

Knickspannung für Grauguss

 d vorh=

F K

A SK

(S. 231)

Festigkeitsbedingung

Quetschen

 d vorh=
gilt für



F
 d zul = dF bzw. dB
A
SF
SB

(S. 230)

 F

a:
b:
c:
A:
F:
SK:
λ:
σ d:
σK:

Werkstoffkennwert
Werkstoffkennwert
Werkstoffkennwert
Querschnitt
Kraft
Sicherheit gegen Knicken
Schlankheitsgrad
Druckspannung
Knickspannung

A:
F:
S:
λ:
σ d:
σdB:
σdF:

Querschnitt
Kraft
Sicherheit gegen Bruch / Fließen
Schlankheitsgrad
Druckspannung
Druckfestigkeit
Druck-Fließgrenze

A:
F:
ω:

Querschnitt
Kraft
Knickzahl

ω-Verfahren (Nachrechnung von Druckstäben)

F
⋅  d zul
A

(S. 234)

Bei λ kleiner 20 kein Nachweis nötig!
λ

20

60

80

100

120

140

160

S235

1,04

1,30

1,55

1,90

2,43

3,31

4,32

S335

1,06

1,41

1,79

2,53

3,65

4,96

6,48

Formänderungsarbeit
Formänderungsarbeit bei eindimensionaler Beanspruchung (Zug, Druck)
2
1  1 2
1
wi: spezifische innere Arbeit
wi = ⋅ = ⋅ ⋅E = ⋅⋅
2 E 2
2
E: E-Modul
spezifische innere Arbeit

W i =wi⋅V

für

W i =∫ wi dV

V:
W i:
ε:
σ:

=const.
für

V

≠const.

Volumen
gesamte innere Arbeit
Dehnung
Spannung

Formänderungsarbeit bei Querkraftbeanspruchung
2
1
1  1 2
wi: spezifische innere Arbeit
wi = ⋅⋅= ⋅ = ⋅ ⋅G
2
2 G 2
G: Schubmodul
spezifische innere Arbeit

W i =wi⋅V

für

W i =∫ wi dV
V

V:
W i:
γ:
τ:

=const.
für

≠const.

12 von 14

Volumen
gesamte innere Arbeit
Schubwinkel
Schubspannung

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Formänderungsarbeit bei Biegebeanspruchung
l
M b2
1
E:
W i = ⋅∫
dx (S. 238)
I:
2 0 E⋅I

Elastizitätsodul
Flächenmoment der Biegung
Mb: Biegemoment
W i: gesamte innere Arbeit

Formänderungsarbeit bei Torsionsbeanspruchung
l
M2
1
G: Schubmodul
W i = ⋅∫ t dx (S. 238)
I:
Flächenmoment der Torsion
2 0 G⋅I
Mb: Torsionsmoment
W i: gesamte innere Arbeit

Energiemethoden
Verfahren von Castigliano
∂ M b  x
l M b  x⋅
dW
∂F
=∫
dx= y
dF 0
E  x⋅I  x
∂ M b  x
M b  x⋅
dW
∂M
=∫
dx=
dM 0
E  x⋅I  x
l

(S. 244)

(S. 244)

y:
E:
F:
I:
M:
W:
φ:

Durchbiegung an Kraftangriffsstelle
Elastizitätsmodul
Kraft
Flächenmoment
Moment
gesamte innere Arbeit
Winkel der Durchbiegung

Verfahren von Menabrea
Berechnung von Auflagergrößen bei statisch unbestimmten Systemen.

∂ M b  x
M b  x⋅
∂ Li
dW
=∫
dx=0
dLi 0
E  x⋅I  x
l ges

(S. 249)

E:
I:
L:
M:
W:

Elastizitätsmodul
Flächenmoment
zusätzliche Auflagergrößen
Moment
gesamte innere Arbeit

Bauteilfestigkeit bei Schwingbeanspruchung
Kerbwirkungsfaktor

 K = D (S. 253)
 DK
 K =1 K⋅ K −1

(S. 253)

k =01

nach Thum

Oberflächenfaktor
D
C O=
D
Bauteiloberfläche

(S. 254)

Probe

Größenfaktor
D
C G=
D

Bauteilgröße

=K 1⋅K 2⋅K 31

(S. 254)

Probe

13 von 14

CO:
CG:
K1:
K2:
K3:
αK:
βK:
ηK:
σD:
σDK:

Oberflächenfaktor
Größenfaktor
Umfeldstützwirkung
Statistik
Größenabhängigkeit der Kerbwirkung
Kerbwirkungsfaktor
Kerbempfindlichkeitszahl
Dauerfestigkeit
Dauerfestigkeit mit Kerbe

Fachhochschule Kempten

Formelsammlung Festigkeitslehre

Überlagerung der Einflußgrößen
 D ⋅C O⋅C G
(S. 254)
 a  zul =
 K⋅S D

SD: Sicherheit gegen Dauerbruch
σa: Ausschlagsspannung

Probe

Beanspruchung umlaufender Bauteile
Rotierender Stab
⋅2 2 2
  x=
⋅ l − x 
2
l=

⋅2 3
⋅l
3⋅E

(S. 255)

(S. 256)



m ⋅l

 max =2⋅ ⋅l 12 2 2
2
A



A:
l:
E:
ρ:
σ:
ω:

Stabquerschnitt
Stablänge
Elastizitätsmodul
Bauteildichte
Spannung
Winkelgeschwindigkeit

r:
E:
ρ:
σ t:
ω:

Bauteilradius
Elastizitätsmodul
Bauteildichte
Tangentialspannung
Winkelgeschwindigkeit

ra:
ri:
r:
E:
ε:
ν:
ρ:
σ:
ω:

Außenradius
Innenradius
Radius an beliebiger Stelle
Elastizitätsmodul
Dehnung
Querkontraktionszahl
Dichte
Normalspannung
Winkelgeschwindigkeit

(S. 256)

nur für Stab mit Punktmasse am Ende

Rotierender Ring
dünn → Beanspruchung in Schalenrichtung

 t =⋅v 2=⋅r 2⋅2
 r=

⋅r 3⋅2
E

(S. 257)

 r =0

(S. 257)

Beanspruchung von Flächentragwerken
Scheiben




r i2 r i2 r 2
3
 r =⋅ ⋅r ⋅
⋅ 1 2 − 2 − 2
8
ra r ra
2

2
a

Radialspannung einer rotierenden Scheibe



(S. 262)

r 2 r 2 13⋅ r 2
3
 t =⋅2⋅r 2a⋅
⋅ 1 i2  i2 −
⋅
8
3 r 2a
ra r
Tangentialspannung einer rotierenden Scheibe

1
r = ⋅  r −⋅ t 
E
1
t = ⋅  t −⋅ r 
E



(S. 261)

Dehnungen der umlaufenden Scheibe

14 von 14