Badanie spręzyny Karol Kraus budownictwo nst .pdf

Sprawozdanie
Ćwiczenie nr 14
Sprężyna

Karol Kraus
Budownictwo I rok
Studia niestacjonarne
Gr. I A

1.Wstęp teoretyczny
Celem wykonanego zadania jest wyznaczenie stałej sprężystości metodą statyczną i
dynamiczna, oraz stwierdzenie prawdziwości prawa Hooke’a
Zjawisko sprężystości polega na tym że ciało po zadziałaniu na nim siłą odkształca się, a gdy
siła przestaje działać ciało wraca do swojego poprzedniego kształtu.

Prawo Hooke’a określa zależnośd odkształcenia od naprężenia. Głosi ono, że odkształcenie
ciała pod wpływem działającej na nie siły jest proporcjonalne do tej siły. Prawo to jest słuszne tylko
w przypadku niewielkich odkształceo.
Naprężenie jest to siła odkształcająca odniesiona do jednostki pola powierzchni, na jaką
działa. Wyznaczamy je wzorem(1.1).
- naprężenie wewnętrzne
Fs-wartośd siły sprężystości
S- płaszczyzna powierzchni przekroju poprzecznego.

Metoda statyczna w tym dwiczeniu polega na zawieszaniu na sprężynie niewielkich
odważników zaczynając od masy 10g., aż do uzyskania masy 160g. Po zawieszeniu odważnika należy
zmierzyd długośd na jaką rozciągnęła się sprężyna. Do wyznaczenia stałej sprężystością ta metoda
posłużymy się wzorem(1.2)

kstat- stała sprężystości
x- odkształcenie
F- Siła sprężystości
Metoda dynamiczna w tym dwiczeniu polega zawieszeniu na sprężynie odważników o
określonych masach a następnie zmierzeniu czasu 20 drgan sprężyny dla każdego z obciążenia. Do
wyznaczenia stałej sprężystości ta metodą posłużymy się wzorem(1.3)

√

2.Opis metody
Na sprężynę zaczepiamy haczyk z ciężarkami, sprężynę doczepiamy do statywu z ruchoma skala(skala
dokładności 1mm) i wybieramy na niej punkt odniesienia (przesuwając skale) tak aby górna częśd
haczyka znajdowała się na początku naszej miarki. Następnie mierzymy wydłużenie sprężyny dla
różnych wartości obciążenia. Drugim naszym pomiarem będzie zmierzeniu czasu 20 drgao sprężyny
dla każdego z obciążenia

Uzyskane wyniki.(tabela1)
Ociązenie(g)
20
40
60
110
160

Wydłuzenie spręzyny(mm)
30
51
77
139
190

Czas drgan(s)
1 pomiar 2 pomiar 3 pomiar średni czas 20 drgao
7,12
7,44
7,38
7,31
8,41
8,26
8,65
8,44
11,24
11,47
11,16
11,29
14,96
14,8
14,94
14,90
17,12
17,13
17,6
17,28

3.Opracowanie wyników
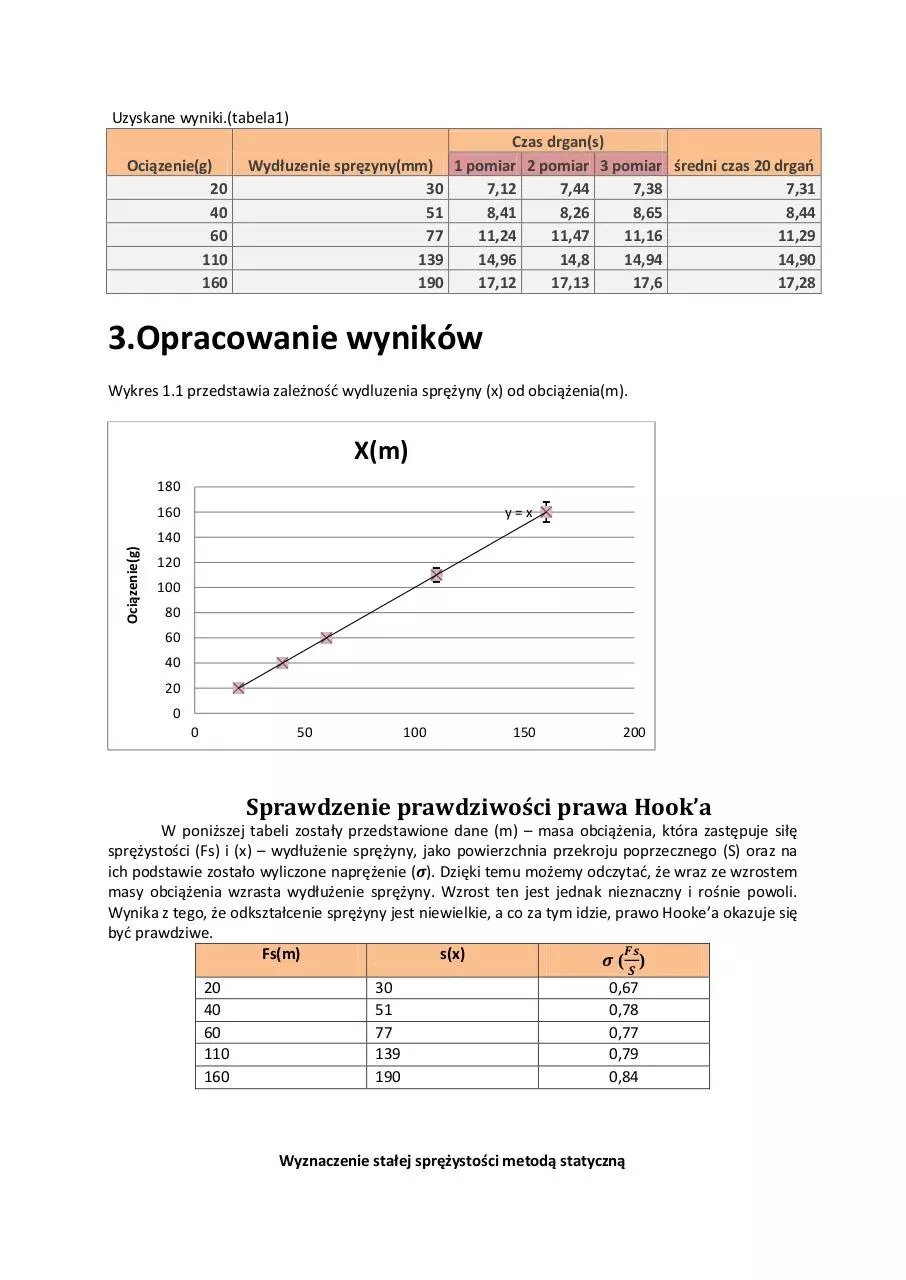
Wykres 1.1 przedstawia zależnośd wydluzenia sprężyny (x) od obciążenia(m).

X(m)
180
160

y=x

Ociązenie(g)

140
120
100
80
60
40
20
0
0

50

100

150

200

Sprawdzenie prawdziwości prawa Hook’a
W poniższej tabeli zostały przedstawione dane (m) – masa obciążenia, która zastępuje siłę
sprężystości (Fs) i (x) – wydłużenie sprężyny, jako powierzchnia przekroju poprzecznego (S) oraz na
ich podstawie zostało wyliczone naprężenie ( ). Dzięki temu możemy odczytad, że wraz ze wzrostem
masy obciążenia wzrasta wydłużenie sprężyny. Wzrost ten jest jednak nieznaczny i rośnie powoli.
Wynika z tego, że odkształcenie sprężyny jest niewielkie, a co za tym idzie, prawo Hooke’a okazuje się
byd prawdziwe.
Fs(m)
s(x)
( )
20
40
60
110
160

30
51
77
139
190

0,67
0,78
0,77
0,79
0,84

Wyznaczenie stałej sprężystości metodą statyczną

W odniesieniu do sprężyn, czy innych ciał o skomplikowanych kształtach do obliczenia stałej
sprężystości korzystamy z wzoru(1.2)

Po przekształceniu otrzymujemy

Wynik przedstawiam w formie tabeli(3)
F(N)

x(cm)

200
400
600
1100
1600

30
51
77
139
199

( )
6,66
7,84
7,79
7,91
8,04

Wynik uśredniony

7,65

Stała sprężystości dla badanej sprężyny wynosi
Wyznaczenie stałej sprężystości metodą dynamiczną
Badana sprężyna porusza się ruchem harmonicznym, współczynnik sprężystości można więc obliczyd
ze wzoru(1.3)

√
Po przekształceniu otrzymujemy

Do obliczenia stałej sprężystości posłużymy się wykresem m(T2). Do sporządzenia wykresu
potrzebujemy danych o czasie jednego drgnięcia sprężyny . Dane przedstawiam w tabeli(4)
m(kg)
0,02
0,04
0,06
0,11
0,16

7,31
8,44
11,29
14,90
17,28

0,73
0,84
1,13
1,49
1,79

0,53
0,71
1,27
2,22
2,99

Wykres(2) przedstawia zależnośd wiążącą masę z okresem

T^2(m)
3,50
y = 18,242x + 0,1229

3,00
2,50
2,00

T^2(m)

1,50

Liniowy (T^2(m))

1,00
0,50
0,00
0

0,05

0,1

0,15

0,2

Korzystając z naszego wykresu oraz ze wzoru(1.3), możemy przystąpid do obliczania stałej
sprężystości metodą dynamiczną. Odczytujemy z wykresu współczynnik kierunkowy:
Ze wzoru
Wyznaczamy

Przyrównujemy nasz współczynnik kierunkowy

do

i wyznaczamy k.

Podstawiając dane do wzoru otrzymujemy

Obliczenie niepewności pomiarowej
Podczas padania sprężyny zaszła niepewnośd pomiarowa przy mierzeniu czasu drgao sprężyny dla
każdego obciążenia. Niepewności te przedstawię w formie tabeli

Obciążenie
(g)
20
40
60
110
160

Wartośd
T20maksymalne T20minimalne średnia
7,44
8,65
11,47
14,96
17,6

7,12
8,26
11,16
14,8
17,12

7,31
8,44
11,29
14,90
17,28

Dodatnia
bezwzględna
niepewnośd
pomiarowa
0,19
0,18
0,13
0,1
0,16

Ujemna
bezwzględna
niepewnośd
pomiarowa
-0,19
-0,18
-0,13
0,1
0,16

Względna
wartośd
pomiarowa
2,6%
2,1%
1,2%
0,6%
0,9%

4.Wnioski
Współczynnik
w stosunku do
różni się znacznie pomimo faktu,
że badana była ta sama sprężyna z tymi samymi obciążeniami.
Druga metoda wyznaczania współczynnika sprężystości, obarczona jest dużym błędem. Podczas
mierzenia drgao sprężyna kołysze się na boki co ma duży wpływ na dokładnośd pomiaru, metoda ta
opiera się na ruchu harmonicznym, który w tym przypadku zostaje mocno zakłócony i powoduje
rozbieżnośd wyniku. Zatem pierwsza metoda wydaje się bardziej wiarygodna.

4.Literatura
http://www.fizykon.org/statyka_osr_ciagle/sprezystosc_stala_sprezystosci.htm
http://pl.wikipedia.org/wiki/Modu%C5%82_Younga