Trabajo Integrador de Matemática (PDF)

Lucas Bois

Franco Gerez

Trabajo Integrador de Matemática
Pautas de investigación
1. Se debe seleccionar al menos uno de los contenidos matemáticos de la siguiente lista:

- Cónicas: Circunferencia, parábola, elipse, hipérbola.
- Funciones: exponenciales y logarítmicas
- Sucesiones
2. Realizar una investigación sobre el tema elegido.
3. Preparar una presentación con el programa “Prezi” o “PowerPoint”, para dar a conocer la
información obtenida.
- La presentación debe incluir:
a) Recorrido histórico sobre el contenido matemático.
b) Reconocimiento de los matemáticos que se destacan en esa área.
c) Ejemplo de aplicaciones.
4. Entregar al profesor por medio de pendrive o subir a un servidor web. En el caso de subirlo a la
web, se deberá enviar el link correspondiente al mail: gdg11007@gmail.com indicando el grupo
y el curso.

Cónicas:
- Hipérbola:
Se llama hipérbola al lugar geométrico de los puntos tales que la diferencia en valor
absoluto de sus distancias a dos puntos fijos llamados focos es igual a una constante menor
que la distancia entre los focos.
En símbolos:
H = {( 𝜒, 𝛾) ∈ ℜ2 ∶ | 𝑑(( 𝜒, 𝛾), 𝐹1 ) − 𝑑((𝜒, 𝛾), 𝐹2 )| = 2𝑎}
Siendo F1 (χ1, γ1) y F2 (χ2, γ2) los focos y 2 a, la constante.
Para deducir la ecuación de la hipérbola se toma como eje 𝜒 a la recta que pasa por los
focos y como eje 𝛾 a la recta perpendicular al eje 𝜒 por el punto medio del segmento F1, F2.
Considerando F1 (c,0) y F2 (-c,0) y planteando la condición impuesta en la definición
se llega a:
𝑥2

eje 𝜒 .

𝑎2

𝑦2

− 𝑏2 = 1 Ecuación canónica de la hipérbola con centro en el origen y eje focal

a se llama semieje real
b se llama semieje imaginario
Se llaman vértices de la hipérbola a las intersecciones de la misma con el eje 𝜒 .
𝛾=0 ⇒

𝑥2
= 1 ⇒ |𝑥| = |𝑎| ⇒ 𝑥 = ± 𝑎
𝑎2
V1 (a,0) y V2 (-a,0)

1

Lucas Bois

Franco Gerez

La hipérbola no intersecta al eje 𝛾, aunque algunos autores llaman vértices ficticios o
imaginarios a:
𝑉3 (0, 𝑏) Y 𝑉4 (0, −𝑏)
Relación entre 𝑎, 𝑏 y 𝑐
En el caso de la hipérbola la relación entre a, b y c está dada por 𝑐 2 = 𝑎2 + 𝑏 2
pudiendo ser 𝑎 > 𝑏, 𝑎 = 𝑏, o 𝑎 < 𝑏.
Como para la elipse, la excentricidad de la hipérbola está definida por:
𝑐
+√𝑎2 + 𝑏 2
ℯ=
⇒𝑒=
>1
𝑎
𝑎
Cuanto menor sea la excentricidad más “cerradas” serán las dos ramas de la hipérbola.
Asíntotas
Se dice que una recta es asíntota de una curva si la distancia entre la recta y la curva
tiende a cero cuando 𝑥, y o ambas tienden a infinito.
En el caso de la hipérbola se comprobará que existen dos asíntotas de ecuación.

𝑦=

𝑏
𝑎

𝑥

𝑏

𝑦=− 𝑥
𝑎

Ejemplo:
16𝑥 2 − 9𝑦 2 = 144
16𝑥 2 9𝑦 2
−
=1
144 144
𝑥2 𝑦2
−
=1
9 16
𝑎2 = 9 ⇒ 𝑎 = 3
𝑏 2 = 16 ⇒ 𝑏 = 4
𝑐 (0,0)
𝑐 2 = 9 + 16 ⇒ 𝑐 = 25 ⇒ 𝑐 = 5
𝑉1 (3,0) 𝑉2 (−3,0)
𝐹1 (5,0) 𝐹2 (−5,0)
5

𝑒=3
𝑦=0

2

Lucas Bois

Franco Gerez
4

𝑦=± 𝑥
3

-

Elipse:
Se llama elipse al lugar geométrico de los puntos de plano tales que la suma de sus
distancias a dos puntos fijos llamados focos es igual a una constante mayor que la distancia
entre los focos.
En símbolos:
𝐸 = {(𝑥, 𝑦) ∈ ℜ2 : 𝑑 ((𝑥, 𝑦), 𝐹1 ) + 𝑑((𝑥, 𝑦), 𝐹2 = 2 𝑎}
Siendo 𝐹1 (𝑥1 𝑦1 ) y 𝐹2 (𝑥2 𝑦2 ) los focos y 2 a la constante.
Para reducir la ecuación de la elipse se toma como eje 𝑥 a la recta que pasa por los
focos y como eje 𝑦 a la recta perpendicular al eje 𝑥 por el punto medio de 𝐹1 , 𝐹2 .
Considerando 𝐹1 (𝑐, 0) y 𝐹2 (−𝑐, 0) y planteando la condición impuesta en la
definición se llega a:
𝑥2

𝑦2

𝑎

𝑏2

+
2

=1

(𝑎 > 𝑏)

Ecuación canónica de la elipse.

a se llama semieje mayor
b se llama semieje menor
Se llaman vértices de la elipse a las intersecciones de la misma con los ejes.
𝑥2
= 1 ⇒ |𝑥| = |𝑎| ⇒ 𝑥 = ± 𝑎 ⇒ 𝑉1 (𝑎, 0) 𝑉2 (−𝑎, 0)
𝑎2
𝑦2
𝑥 = 0 ⇒ 2 = 1 ⇒ |𝑦| = |𝑏| ⇒ 𝑥 = ± 𝑏 ⇒ 𝑉3 (0, 𝑏) 𝑉4 (0, −𝑏)
𝑏

𝑦=0⇒

Relación entre 𝑎, 𝑏 y 𝑐:
Siendo 𝑉3 (0, 𝑏) un punto de la elipse debe verificar la definición, lo que
implica:
𝑑 (𝑉3 , 𝐹1 ) + 𝑑 (𝑉3 , 𝐹2 ) = 2 𝑎
𝑑 (𝑉3 , 𝐹1 ) + 𝑑 (𝑉3 , 𝐹2 )
𝑑 (𝑉3 , 𝐹1 ) + 𝑑 (𝑉3 , 𝐹2 ) = 𝑎
Excentricidad:
La excentricidad caracteriza la forma de la elipse. Se la representa por 𝑒 y se
define 𝑒 =

𝑐

𝑎

.

Teniendo en cuenta que: 𝐶 = +√𝑎2 − 𝑏 2 se tiene: 𝑒 =

+√𝑎2 −𝑏2
𝑎

Ejemplo:
Semieje mayor
Semieje menor

𝑎2 = 25 ⇒ 𝑎 = 5
𝑏2 = 9 ⇒ 𝑎 = 3

Coordenadas del centro
(0,0)
Coordenadas de los vértices 𝑉1 (5,0) 𝑉2 (−5,0) 𝑉3 (0,3) 𝑉4 (0, −3)
Relación entre 𝑎, 𝑏 y 𝑐
𝑐 2 = 𝑎2 − 𝑏 2 ⇒ 𝑐 2 = 25 − 9 ⇒ 𝑐 2 = 16 ⇒ 𝑐 = 4

3

Lucas Bois

-

Franco Gerez

Coordenadas de los focos

𝐹1 (4,0)

Excentricidad

𝑒=

Ecuación de eje focal

𝑦=0

𝑐
𝑎

𝐹2 (−4,0)

=

4
5

Circunferencia:
Se llama circunferencia al lugar geométrico de los puntos del plano tales que
su distancia a un punto fijo, llamado centro, es constante.
La constante se indica con 𝑟 y se llama Radio de la circunferencia. El punto
fijo es 𝐶 (ℎ, 𝑘).
En símbolos:
𝐶 = {(𝑥, 𝑦) ∈ ℜ2 : 𝑑((𝑥, 𝑦), (ℎ, 𝑘)) = 𝑟}
Sea 𝑃(𝑥, 𝑦) un punto genérico. La distancia del centro a cualquier punto P
genérico es igual al módulo del vector → . Entonces resulta:
𝐶𝑃

‖→ ‖ = +√(𝑥 − ℎ)2 + (𝑦 − 𝑘)2 = 𝑟
𝐶𝑃

Y elevado al cuadrado se obtiene:
(𝑥 − ℎ)2 + (𝑦 − 𝑘)2 = 𝑟 2 Ecuación de la circunferencia
con 𝐶(ℎ, 𝑘) y Radio r.
Si el centro coincide con el origen de coordenadas, la ecuación queda de la
siguiente forma:
𝑥 2 + 𝑦 2 = 𝑟 2 Ecuación canónica de la
circunferencia con 𝐶(0,0) y Radio r.
Ejemplo:
𝑥 2 − 3𝑥 + 𝑦 2 + 2𝑦 − 3 = 0

𝑟=

5
2

3

𝐶 ( , −1).
2

4

Lucas Bois

-

Franco Gerez

Parábola:
Se llama parábola al lugar geométrico de los puntos del plano que equidistan de un
punto fijo llamado foco y de una recta fija llamada directriz.
En símbolos:
𝑃 = {(𝑥, 𝑦) ∈ ℜ2 : 𝑑 ((𝑥, 𝑦), 𝐹) = 𝑑((𝑥, 𝑦), 1}
Para deducir la ecuación de la parábola, se toma como eje 𝑦 al que pasa por el
foco y es perpendicular a la directriz. Como eje 𝑥 se toma al paralelo a la directriz,
que está del foco a una distancia igual a la mitad de la distancia del foco a la directriz.
Si

1
2𝑃

= 𝑎 queda 𝑦 = 𝑎 𝑥 2

Ecuación canónica de la parábola.

La recta perpendicular a la directriz que contiene al foco se llama eje de la
parábola.
El punto en que la parábola corta su eje se llama vértice.
Si a > 0 entonces y > 0 y como x toma todos los valores reales resulta una curva
abierta en el semiplano superior que se extiende indefinidamente.
Si a < 0 entonces y < 0 resulta una curva abierta en el semiplano inferior.
Excentricidad:
Siendo la definición general de la
excentricidad de una cónica la relación entre las
distancias de un punto P al foco y de P a la
directriz, en el caso de la parábola resulta igual a
uno.
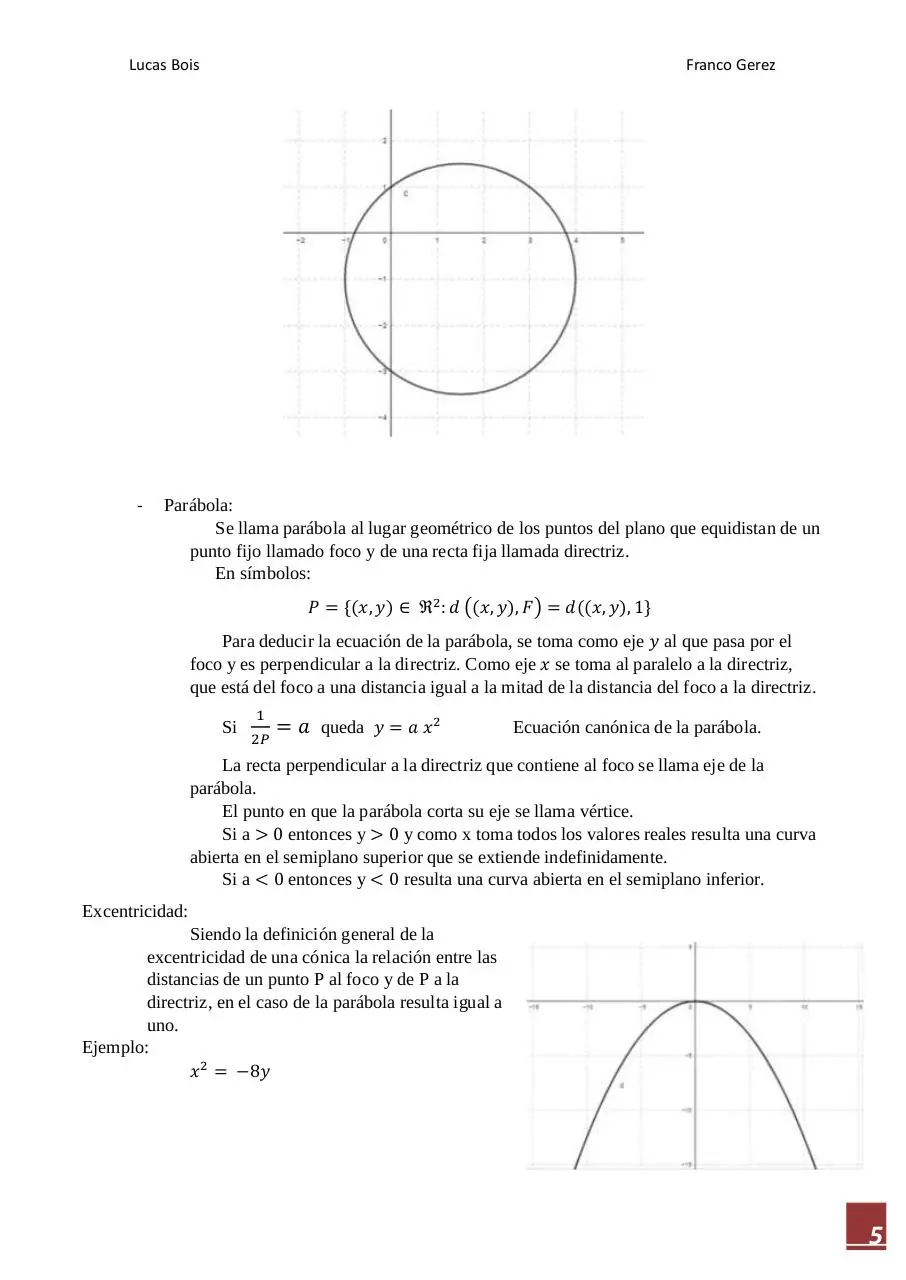
Ejemplo:
𝑥 2 = −8𝑦

5